FULL PAPER PUBLCIATION CAN BE SEEN HERE:
Published work in Brain and Cognition:
Shaw, S. B., McKinnon, M. C., Heisz, J., & Becker, S. (2021). Dynamic task-linked switching between brain networks–A tri-network perspective. Brain and cognition, 151, 105725.
~~
Recent studies have proposed a triple-network model of how the human brain functions. Different cognitive tasks are correlated with activity in distinct brain networks. Spatially accurate neuroimaging techniques are used to identify activation of these networks. Our research examines whether neuroimaging techniques high in temporal resolution could provide a meaningful representation of the intrinsic networks. Participants had simultaneous functional magnetic resonance imaging (fMRI) and electroencephalography (EEG) recordings done while performing network-specific cognitive tasks. Asymmetric fMRI-EEG analysis was done for correlation measures between modalities. We use phase-phase cross-frequency coupling (CFC) for pre-processing EEG into meaningful input features for subsequent cross-modality (EEG-fMRI) subsequent analysesdue to its success in examining large-scale brain activation. A support vector machine classifier was then taught on the CFC values. Results showed an 80% percent accuracy for a 5-way classification. Further research implementing additional statistical input features could achieve better accuracy. This paves the way for future research in precise measures of network activation without spatially-accurate neuroimaging methods
Data analysis overview
Data Analysis
To record CFC across the brain, a measure of synchrony between two continuous time series of brain activity had to be produced. Synchronization indices represent CFC in a way that can be statistically assessed over time, experimental conditions, trials, and subjects.
EEG data was filtered into six frequency bandwidths: delta, theta, alpha, beta, gamma, and high gamma. Time windows were redefined to include a 250ms overlap. This improves accuracy and prevents edge-effect artifacts. To measure cross-frequency coupling, higher frequencies and lower frequencies were looped for each participant and their sessions. This was done for all combinations of the six frequency bandwidths. First, a Hilbert transform, analogous to a Fast Fourier Transform, was used to calculate the upper frequency power time series for each window. Lower frequency measurements were filtered using the MATLAB Hilbert transform method as well. Angle projections of the real and imaginary components needed to be calculated next. The arctan of the higher frequency power series and Hilbert-filtered lower frequency data components provided measures of phase values. The phase of the lower frequency band was computed directly from the signal. Calculation of the higher frequency band’s phase was different and used a power time series of the original signal. Synchronization index (SI) values were then calculated and recorded using the equation in Figure 1.
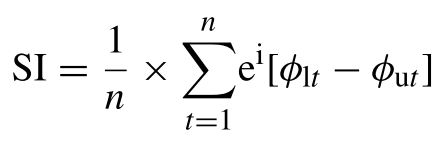
Project 4: Formula used for synchronization index, SI. φut represents the upper frequency power time series’ phase values at time t. The phase value of the lower frequency is φIt, and n is the amount of time points.
SI values were used to identify the three intrinsic networks with a support vector machine (SVM) classifier. The classifier was trained with an 80/20 split. 80 percent of the dataset was used for training, and 20 percent for testing. We used 10-fold testing for a more precise indication of prediction accuracy. Different results were averaged to give us our final network prediction accuracy. This was all done with the svm() method in MATLAB.
Graphs displaying general results:
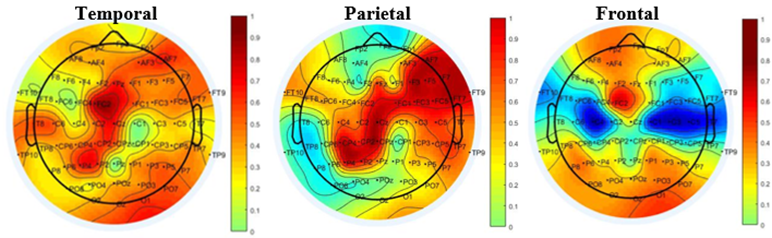
Project 4: Theta-gamma CFC SI values plotted using channels in the temporal (T7), parietal (P7), frontal (F7) lobes as high frequency.